今天的數學知識含量高，請小心服用。

碎形

自然界與人類的生活環境中，有許多自我相似的圖形。如果我們將海岸不斷的放大，都會和原來圖形的某個部分相似（至少近似的）；將股票的年線圖也會和月線圖、日線圖有相似的情形。而「碎形」則是研究這種具有自我相似特性圖形的主題，也是計算機圖學一個類別。

我們一般的空間維度都是整數維度，線的維度是1，平面的維度是2，空間的維度則是3；碎形維度則是推擴了維度的觀念，除了整數維度外，也能定義分數維度，像底下Koch曲線的碎形維度是1.26。

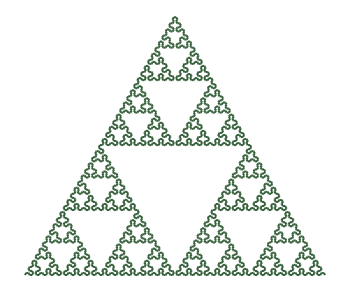
其實數學家早在計算機發明之前便發想過類似的奇異圖形，像是Sierpinski triangle和類似雪花形狀Koch curve。

Koch曲線甚至在民國84年的時候被設計成大學入學考試的題目。

今天，我們就來做做Koch曲線的主題教學製作。

繪圖原理

• 繪製一個正三角形。
• 取底邊切成均分的三段。
• 將中間一段以左端點為中心，逆時針旋轉60度；再以右端為中心，順時針旋轉60度，用這兩段取代中間的一段。
• 再將底邊得到的圖形，以三角形的左端點為中心，逆時針旋轉60度；再以右端為中心，順時針旋轉60度，即可得到第二層的圖形。
• 依上述原則，依序畫第三層、第四層、...的圖形。

程式規劃

我們在utilities.js中寫好內插法公式和點內插函式。

export function interpolatePoint(point1, point2, ratio) {
  return board.create(
    'point',
    [
      () => interpolate(point1.X(), point2.X(), ratio),
      () => interpolate(point1.Y(), point2.Y(), ratio),
    ],
    {
      withLabel: false,
      visible: false
    }
  )
}

export function interpolate(t1, t2, ratio) {
  return t1 * (1 - ratio) + t2 * ratio
}

再利用一個陣列A存放不同層的圖形，陣列每個元素是一包含middle、left和right三個屬性物件，每個屬性的值是一個陣列存放線段（segments），再用一個currentIndex的變數綁定各層圖形的顯示。

function drawKoch(i) {
  A[i] = {middle: [], left: [], right: []}
  A[i - 1].middle.forEach(seg => {
    const pivot1 = interpolatePoint(seg.point1, seg.point2, RATIO)
    const pivot2 = interpolatePoint(seg.point1, seg.point2, RATIO * 2)
    const seg1 = board.create('segment', [seg.point1, pivot1])
    const seg4 = board.create('segment', [pivot2, seg.point2])
    seg1.setAttribute({ color: '#37613C', visible: () => currentIndex === i })
    seg4.setAttribute({ color: '#37613C', visible: () => currentIndex === i })
    const rotate1 = board.create('transform', [Math.PI * 2 / 3, pivot1], { type: 'rotate' })
    const rotate2 = board.create('transform', [Math.PI * 4 / 3, pivot2], { type: 'rotate' })
    const seg5 = board.create('segment', [seg1, rotate1], { color: '#37613C', visible: false })
    const seg2 = board.create('segment', [seg5.point2, seg5.point1], { color: '#37613C', visible: () => currentIndex === i })
    const seg6 = board.create('segment', [seg4, rotate2], { color: '#37613C', visible: false })
    const seg3 = board.create('segment', [seg6.point2, seg6.point1], { color: '#37613C', visible: () => currentIndex === i })
    A[i].middle.push(seg1)
    A[i].middle.push(seg2)
    A[i].middle.push(seg3)
    A[i].middle.push(seg4)
  })
  A[i].left = A[i].middle.map(seg => {
    let segTemp = board.create('segment', [seg, rotateA60], {visible: false})
    return board.create('segment',[segTemp, reflectAC] , { color: '#37613C', visible: () => currentIndex === i })
  })
  A[i].right = A[i].middle.map(seg => {
    let segTemp = board.create('segment', [seg, rotateB300], {visible: false})
    return board.create('segment', [segTemp, reflectBC], { color: '#37613C', visible: () => currentIndex === i })
  })

}

今天的程式裏用到了Javascript陣列的map方法，使用方式和forEach差不多，好處是可以自動得到一個陣列。

程式原始碼

今日程式原始碼
KochCurve
Sierpinski

今日小結

今天數學含量太高，自己都已經有些昏頭了，相信看得了也是快睡著了，希望世界以後不要再有數學這個科目，害死大家了。不過，現在世界的電腦科技發展已經很好，有很多輔助的媒體來幫忙我們，大家加油，明天見！